Posted by 2 min read ~ Hello readers! It’s really important for me to continue my practice and learning. Every week, I block off 30 minutes, set a timer and choose a challenge from codewars. This helps me keep my skills sharp, see how other devs all over the planet would solve these problems, and take some leisure time to problem solve and be creative. Being able to see other solutions expands my mind for solving future problems in a clever and efficient way. Today, the problem set focuses on Python.
Jamie is a programmer, and James’ girlfriend. She likes diamonds, and wants a diamond string from James. Since James doesn’t know how to make this happen, he needs your help.
Task
You need to return a string that looks like a diamond shape when printed on the screen, using asterisk (*) characters. Trailing spaces should be removed, and every line must be terminated with a newline character (\n).
Return null/nil/None/... if the input is an even number or negative, as it is not possible to print a diamond of even or negative size.
Examples
A size 3 diamond:
*
***
*
…which would appear as a string of " *\n***\n *\n"
A size 5 diamond:
*
***
*****
***
*
…that is:
" *\n ***\n*****\n ***\n *\n"
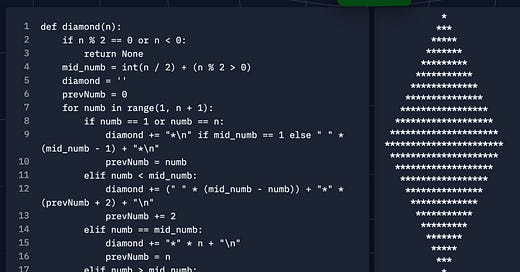
def diamond(n):
if n % 2 == 0 or n < 0:
return None
mid_numb = int(n / 2) + (n % 2 > 0)
diamond = ''
prevNumb = 0
for numb in range(1, n + 1):
if numb == 1 or numb == n:
diamond += "*\n" if mid_numb == 1 else " " * (mid_numb - 1) + "*\n"
prevNumb = numb
elif numb < mid_numb:
diamond += (" " * (mid_numb - numb)) + "*" * (prevNumb + 2) + "\n"
prevNumb += 2
elif numb == mid_numb:
diamond += "*" * n + "\n"
prevNumb = n
elif numb > mid_numb:
diamond += (" " * (numb - mid_numb)) + "*" * (prevNumb - 2) + "\n"
prevNumb -= 2
return diamond
First, I excluded out the even numbers and numbers that were less than 0 because we don’t need to worry about evaluating those. Next, I decided to approach this through finding the mid point (median) of the odd number that represents, n.
Let’s say that your given number is 11. The purpose of the mid_numb variable is to find the median of this number like below:
1 2 3 4 5 6 7 8 9 10 11
My thought process was that once you determine the median, you can build your diamond “up and down” using that as your main point of reference to know where you are in the building process of the algorithm. For the iterator, I use a standard range loop but start at 1 and go to n + 1. When building my if statements, I had to factor in a few things such as how many spaces needed to be added as you build the diamond as well as how many stars are needed to make up a given line of the diamond itself. For the first problem, the mid_numb variable came into play nicely because while the iterator was less/greater than the midpoint, I could increase/decrease the amount of spaces needed for the diamond to eventually make its way to the end point and back to origin to complete the overall shape of the diamond. For the actual number of stars needed, I was able to use a simple variable to store where the number was at the point of iteration and continuously add or detract from the midpoint based on where I was within the procedure. I was a big fan of this challenge and hope that you find it interesting too!
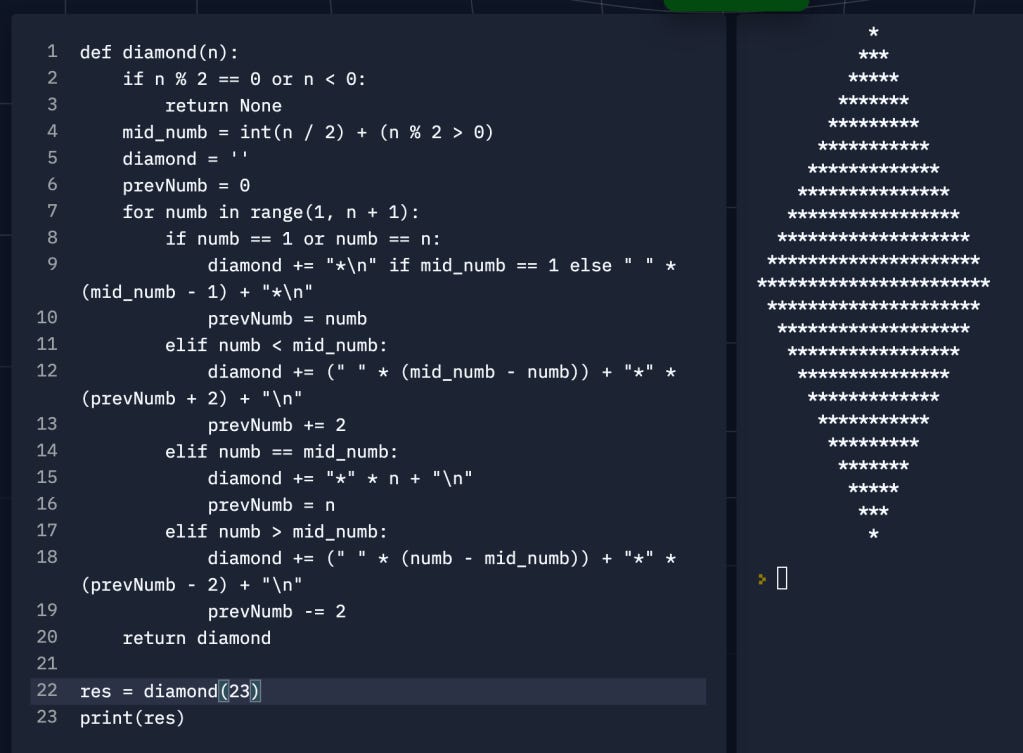
Here is how it looks when you plug a random odd number in:
All solutions are also now on my GitHub profile if you want to check out all of the coding challenges I’ve completed so far!
All credit to problem sets goes to codewars
Another Coding Blog 